Cori, my oldest daughter and Kali, one of her close friends at SVS, are having a good-humored debate about which one of them reads more books. This debate has been going on so long now that for Christmas their friends bought them each a special coffee mug that supports their side of the argument. They both read a lot. There is no surprise here, many SVS students are avid readers. I have a niece who graduated from SVS close to 10 years ago who reads a great deal. My brother-in-law, who graduated from SVS over 40 years ago, to this day always has a book in hand. It’s not necessary to have English, History and Art teachers giving kids reading assignments. Drawn by their own interests and curiosity, children will find books to read. In fact, I think it is pretty clear that having teachers dictate what books to read, and often the pace at which they should be read, has a negative impact on kids’ interest in reading.

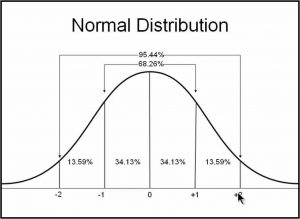
At the last parent teacher conference while my youngest daughter Holly was in public school, the teacher explained to me that that she was a little worried about Holly’s reading level. She said that by that week of the school year Holly should be at level K, but she was currently only at “J”. I was uncomfortable with this at the time, but it took me a while before I realized why. For much of my career I worked in medical and social research. At the heart of statistical analysis used in that field is the idea that the measurement of most social and medical phenomena can be represented as a “normal distribution”. For any collection of normally distributed data, a standard deviation can be calculated that effectively slices up the normal distribution such that 68% of the data is within 1 standard deviation of the average, and 95% of the data are within 2 standard deviations of the average. The important take home message here is that when measuring anything in the social or scientific world where some degree of variation is expected, it will be “normal” for most of the data to be something other than average. Some thirty percent will be some distance from average and 5% will be quite far from average and that is the very definition of “Normal Distribution”! So for pretty much anything you look at, it is normal for 5% (or one in 20) to be “far” from average.

The Fountas-Pinnell Guided Reading system uses the A-Z scale to divide expected reading levels from Kindergarten through 6th grade into 26 levels. During each grade of school, children are expected to move through multiple levels of this system. A quick search on Google reveals that some children start to read at age 4, most will be reading by age 7 and some will not read until they are even older. To me that indicates that the normal distribution related to reading encompasses years, not weeks. To suggest that a student is not performing to expectations for failing to move between one of the reading categories and the next by a certain week of elementary school is not “normal”.

Cori, now 17, has been a voracious reader from a very young age. While Kali, now 13, came later to reading. Her mother wrote an SVS blog article about watching as one of her twins took to reading while the other twin, Kali, chose to wait. I find it inspiring to see that Cori, who has been reading for 10 years, and Kali, who has probably only been seriously reading for maybe 4 years, are now vying over the title of “who reads more”. It shows that the path to achievement can be unique for each kid. No one path is superior to another.
Children need not be held to the tyranny of the average. Just because you can calculate the average age at which a group of children achieve a certain reading ability, does not mean it is wise to try to force all children to conform to that average. Averages are mathematical constructs and should be not thought of as moral guideposts.

For reasons of family peace, I will decline to weigh in on the “Who Reads More” debate between Cori and Kali. But I do know that they both read a great deal, far more than I did at their age.